Nonlinear Oscillations
Intermodulation
In Nanoscience and in Quantum Technology, high quality factor resonators are used to make very sensitive measurements. One measures how the resonance is perturbed when it is coupled to the system of interest. Our reserach centers around a particular way of measuring this perturbation, which we call Intermodulation Spectroscopy [1].
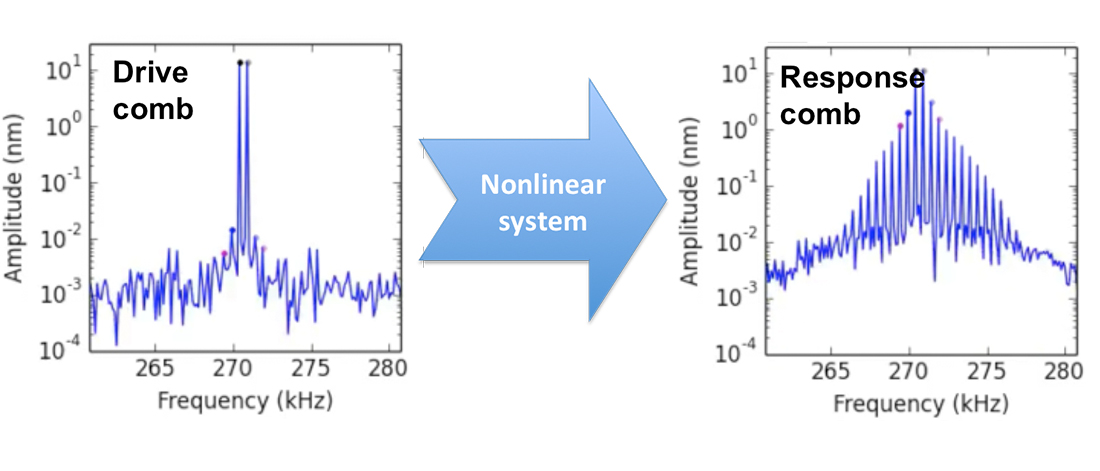
Intermodulation, also known as frequency mixing, happens in nonlinear systems when they are driven by more than one tone. By tone we mean a pure sinusodial oscillation, specified by a frequency, amplitude and phase (or alternatively, a frequency and two quadrature amplitudes). Often intermodulation is considered in a negative context, such as Intermodulation distortion (IMD) in radio sytems, where nonlinearity causes unwanted signals to appear in some frequency band where they are not suppose to be. However, intermodulation is also at the heart of very pleasing sensations, for example the feeling one has when hearing an orchestra strike a perfect cord, or a choir singing in perfect harmony. Musical consonance happens when the all the tones generated by the musical instruments, and all their mixing products produced by the nonlinear transduction of sound by our ears, are all integer multiples of one base tone called the musical key.
In technical terms: When a nonlinear system is driven with multiple tones at frequencies \(f_1, f_2, f_3, \dots\), it will generate intermodulation products, or response tones at frequencies \(f_\text{IMP}=n_1f_1+n_2f_2+n_3f_3+\dots\) ... , where \(n_1,n_2,n_3,\dots\) are any integer. A perfect harmony arises when we tune the drive tones, choosing them to be integer multiples of one base tone \(\Delta f \), such that \(f_1=k_1\Delta f, \space f_2=k_2\Delta f, \space f_3=k_3\Delta f \dots\), where \(k_1,k_2,k_3,\dots\) are integers. In this case all the intermodulation products generated by the nonlinearity will also be located at frequencies which are integer multiples of \(\Delta f\). The base tone \(\Delta f\) is the key, or root tone, from which all drive tones and their mixing products are derived. Signals with many components at frequencies that are integer multiples of one base tone are known as stablized frequency combs. In the time domain, frequency combs are simply periodic waveforms, with period \(T = \frac{1}{\Delta f}\).
Having one base tone is highly advantageous for experiments because we may use the base tone \(\Delta f\) as a reference oscillation for lockin measurement [2] of the amplitude and phase at all response tones. Lockin measurement with a very stable reference oscillation is the heart and soul of precision measurement. We have designed a unique digital instrument for locking in on frequency combs, which we call the Intermodulation Lockin Amplifier (ImLA) [3], or Multifrequency Lockin Amplifier (MLA). A spin-off company called was formed with the mission to supply this instrument to other laboratories.
Applications
The intermodulation measurmement paradigm has very broad and general applicability. We work with two application areas: where the high Q resonator is a vibrating cantilever at several hundred kHz and the nonlinearity is the intereaction between a sharp tip and a surface, and where the resonator is a superconducting structure with characteristic frequencies of several GHz and the nonlinearity is a Josephson tunnel junction or weak link. The former application is in the classical regime, where the resonator's thermal equilibrium fluctuation energy \(k_\text{B}T\) is much larger than its zero-point quantum fluctuation energy \(\frac{1}{2}hf_0\). The latter application, when measured at very low temperature, can be put in the quantum regime where \(k_\text{B}T<\frac{1}{2}hf_0\). In both regimes our detectors and amplifiers are able to resolve the limiting thermal, or quantum fluctuation energy. One of our areas of interest is to understand how nonlinearity and measurement influences these measurement-limiting fluctuations.
References:
[1] Reconstructing Nonlinearities with Intermodulation Spectroscopy. C. Hutter, D. Platz, E. A. Tholén, T. H. Hansson and D. B. Haviland. Phys. Rev. Lett., 104, 050801 (2010).
[2] The Measurement of Thermal Radiation at Microwave Frequencies. R. H. Dicke, Rev. Sci. Instr., 17, 268 (1946).
[3] The Intermodulation Lockin Analyzer, E. A. Tholén, D. Platz, D. Forchheimer, V. Schuler, M. O. Tholén, C. Hutter and D. B. Haviland. Rev. Sci. Instr., 82, 026109 (2011).

